この記事では、大学の化学で習う「項の記号」について解説します！
項の記号とは？
項の記号は３つの要素から成り立つ
まず、原子の項の記号はこのような三つの要素から成り立っています。
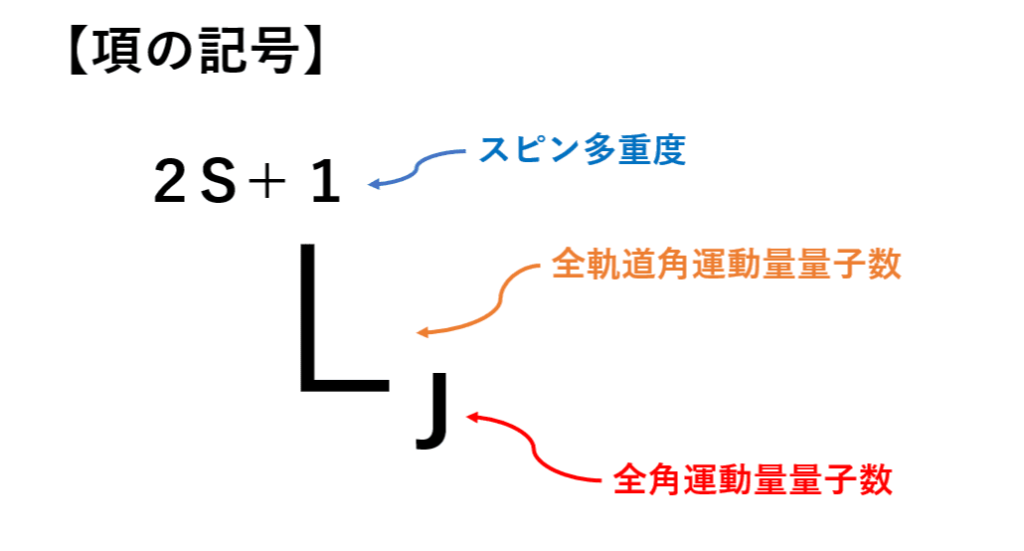
- ２S＋１：スピン多重度
- L：全軌道角運動量量子数
- J：全角運動量量子数
それぞれの要素の求め方
３つの要素から成り立つことが分かったところで、次はそれぞれの要素の求め方を説明していきます。
スピン多重度（２S＋１）
まず、スピン多重度です。
さっきの項の記号の図を見たときに、他はLとかJなのに、スピン多重度だけ２S＋１で、疑問に思った人もいるでしょう。
実は、「２S＋１」というのは、S（全スピン角運動量量子数）を２倍して１足したものです。
LやJの仲間である、Sがいたんですね。（ちなみに、S・L・Jはゼロ以上です。）
ということで、スピン多重度（２S＋１）を求めるための、S（全スピン角運動量量子数）の求め方ですが、例えば２電子の場合、
\(\Large{S = s_1 + s_2 \rightarrow |s_1 – s_2|}\) （ただし整数刻みで、s1, s2は電子のスピン角運動量量子数）
ここで、”→”の意味ですが、たとえばA→Bは「AからBまで」を表します。
また、電子のスピン角運動量量子数は\(\large{-\frac{1}{2}, \frac{1}{2}}\)のどちらで、\(\large{-\frac{1}{2}}\)は↑、\(\large{\frac{1}{2}}\)は↓を表しています。（電子のスピンが”↑“と”↓“の２通りあることはこの記事を読んでいる人なら恐らく知っていると思います。）
さて、ここまで読んでピンときたでしょうか。
正直まだ、大体の人はピンとこないと思います。
ただ、具体例を見てみると、一気に理解が進むはずです！
1s軌道と2s軌道に１つずつ電子が入っているときを考えます。
それぞれの電子のスピン角運動量量子数をs1, s2とすると、
\(\Large{ S = (\frac{1}{2} +\frac{1}{2}), (\frac{1}{2}- \frac{1}{2})}\)の２通りあります。
というわけで、スピン角運動量量子数は
S＝1, 0になります。
したがって、スピン多重度は、
２S＋1＝2＋1, 0 + 1＝3, 1
の２つです。
1s軌道に２つの電子が入っているときを考えます。
それぞれの電子のスピン角運動量量子数をs1, s2とすると、
一見、\(\Large{ S = (\frac{1}{2}+\frac{1}{2}), (\frac{1}{2} -\frac{1}{2})}\)の２通りあるように感じます。
ですが、このうち、\(\Large{ S = (\frac{1}{2}+ \frac{1}{2})}\)は電子が取れない値です。
なぜなら、パウリの排他原理より、２つ以上の電子が同じ量子状態をとることはできないからです。
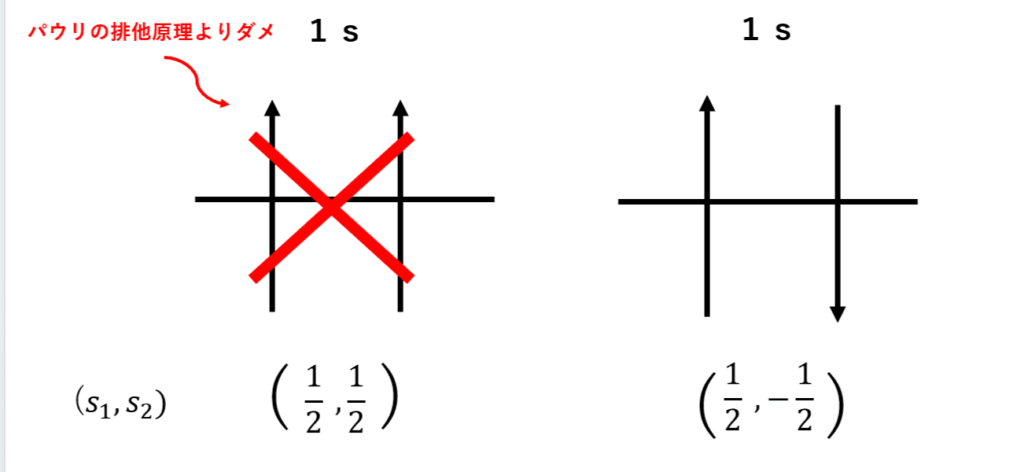
というわけで、スピン角運動量量子数は\(\Large{ (s_1,s_2) = (\frac{1}{2}, -\frac{1}{2})}\)のときの値より、
S＝１になります。
したがって、スピン多重度は、
２S＋１＝0＋１＝1
です。
ちょっとした引っかけ問題でしたね。初見でパウリの排他原理に気付けた人はすごいです。
たまにパウリの排他原理を使うことがあるよ、っていうのがポイントです。
全軌道角運動量量子数（L）
次は全軌道角運動量量子数（L）です。
\(\Large{L = l_1 + l_2 \rightarrow |l_1 – l_2|}\) （ただし整数刻みで、l1, l2は電子の軌道角運動量量子数）
これは、さっきの
\(\Large{S = s_1 + s_2 \rightarrow |s_1 – s_2|}\) （ただし整数刻みで、s1, s2は電子のスピン角運動量量子数）
に似ていますよね！
今回、新たに”l1, l2（電子の軌道角運動量量子数）”が登場しましたが、これらはどう求めてやればいいのでしょうか？
答えは簡単で、s軌道の電子ならl=0、p軌道の電子ならl=1、d軌道の電子ならl=2、…
というように軌道の名前と対応して、１ずつ大きくなっていきます。
| 軌道角運動量量子数(l) | ０ | １ | ２ | ３ |
| 割り当てられるアルファベット（小文字） | ｓ | ｐ | ｄ | ｆ |
lは別名「方位量子数」ともいい、大学では授業の序盤で習う内容です。
全角運動量量子数にも、アルファベット（大文字）が割り当てられています。
| 全軌道角運動量量子数(L) | ０ | １ | ２ | ３ |
| 割り当てられるアルファベット（大文字） | S | P | D | F |
全角運動量量子数でも、練習問題を通して理解を深めていきましょう！
電子は２つとも、ｓ軌道上にあるので、l1, l2ともにゼロです。
したがって、Ｌ＝０＋０→｜０ー０｜＝０です。
対応するアルファベットは”S”になります。
さっきより簡単ですね。
全角運動量量子数（Ｊ）
最後は全角運動量量子数（Ｊ）です。
Ｊの求め方ですが、
\(\Large{J = L+ S \rightarrow |L – S|}\) （ただし整数刻み)
です。
これも、
\(\large{L = l_1 + l_2 \rightarrow |l_1 – l_2|}\) （ただし整数刻み)
\(\large{S = s_1 + s_2 \rightarrow |s_1 – s_2|}\) （ただし整数刻みで)
に似ていますね。
ということは、ＬとＳが分かれば、同じ要領でＪも求められるわけですね！
練習問題
最後に練習問題を置いておきます。
練習問題①
問題
Na(ナトリウム)：[Ne]3s1の項の記号を答えよ。
ただし、[Ne]はネオンの電子配置を指し、項の記号を求めるうえで（ネオンの軌道は埋まってるので）考えなくていい。
解答
\(\Large{s= \frac{1}{2}, l = 0}\)より、
\(\large{S = \frac{1}{2}, 2S+1 =3}\)
\(\Large{L = 0}\) つまり、対応するアルファベットはS
\(\Large{J = \frac{1}{2} + 0 = \frac{1}{2}}\)
よって、項の記号は、3S1/2
練習問題②
問題
He：1s12s1（励起状態）の項の記号を求めよ。
解答
\(\Large{S = s_1 + s_2 \rightarrow |s_1 – s_2|} = \frac{1}{2} + \frac{1}{2}, \frac{1}{2} – \frac{1}{2} = 1, 0\)
よってスピン多重度は
\(\Large{2S+1 = 3, 1}\)
\(\Large{L = l_1 + l_2 \rightarrow |l_1 – l_2| = 0}\)
よって対応するのはS
\(\Large{J = L+ S \rightarrow |L – S| = 1, 0}\)
したがって、項の記号は二つあり、
1S0と3S1である。
これで終わりです。お疲れさまでした！！
コメント