両末端間距離
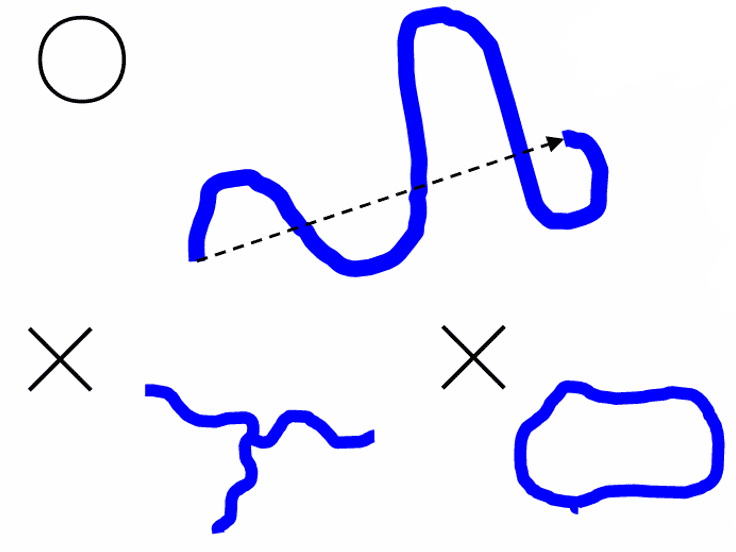
両末端間距離は通常、ベクトル量として表され、高分子鎖の両端(開始点と終点)の距離を指します。
このため、直鎖の高分子のときしか考えることは出来ません。
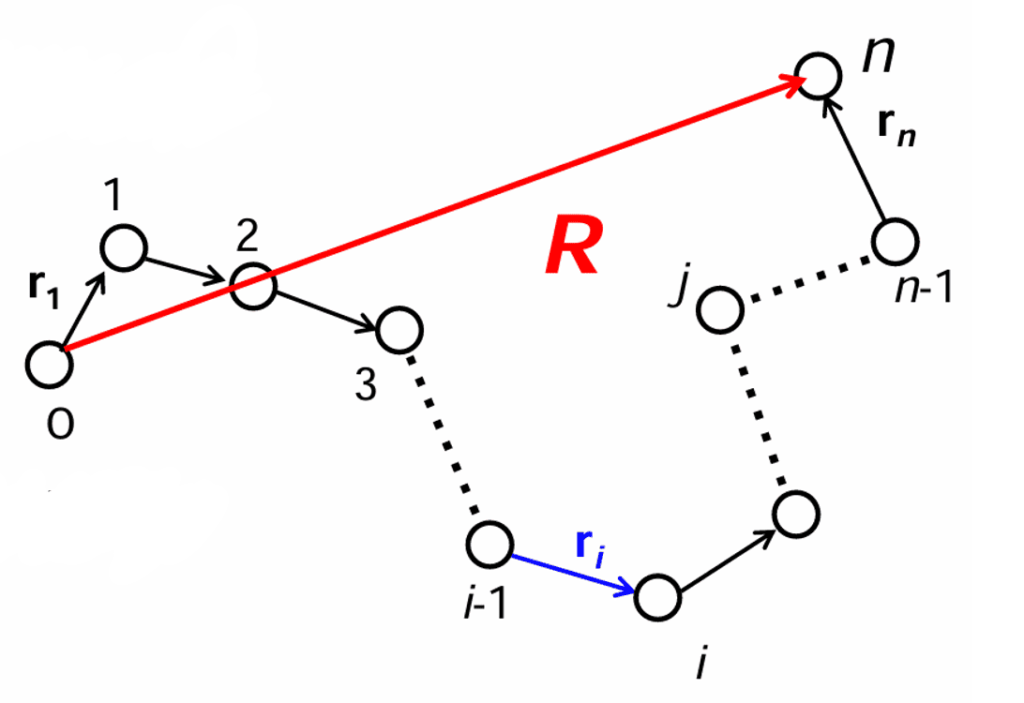
\(\large{\mathbf{R} = \sum_{i=1}^{n} \mathbf{r}_i}\)
ここで、
- \(\mathbf{r}_i\) は各セグメントのベクトル、
- n はモノマー数に比例するもので、鎖のセグメント数です。
ここで一つ問題点があって、実際の高分子は熱運動によってランダムに動くため、両末端間距離 R の平均値はゼロになってしまいます。
そのため、統計的な指標として二乗平均平方根(rms, root mean square) がよく用います。
\(\Large{\langle R^2 \rangle = \langle \mathbf{R} \cdot \mathbf{R} \rangle}\)
(1) 理想鎖の場合
もし高分子が剛直ではなく自由に動けると仮定すると、これはランダムウォークとして扱えます。その場合、各セグメントが独立にランダムな方向を向いているため、両末端間距離の二乗平均平方根は
\(\large{\sqrt{\langle R^2 \rangle} = b \sqrt{n}}\)
となります。ここで、
- bは1つのセグメントの長さ、
- n はセグメントの数です。
この関係はガウス鎖モデルとも呼ばれます。
(2) 理想鎖でない場合(実在鎖)
実際は、分子が完全に自由に動くことは難しく、いろいろな条件によって理想的なガウス鎖よりも分子は大きくなります。
例として、「角度一定で回転は自由にできる」という条件の自由回転鎖を考えてみます。
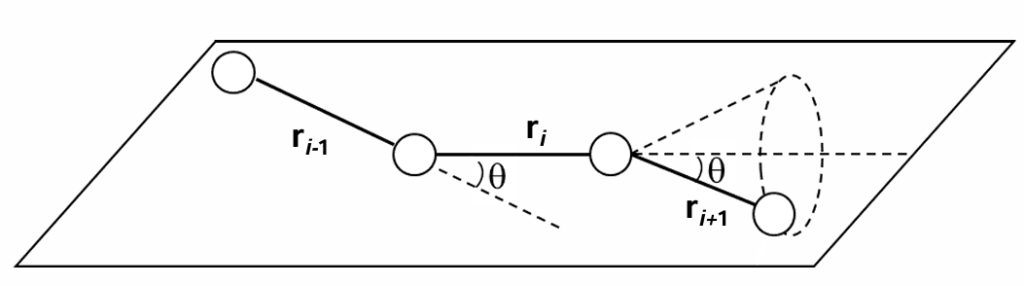
すると、その両末端間距離は以下で表せます。
\(\large{\sqrt{\langle R^2 \rangle} = b \sqrt{n}\frac{1+cos\theta}{1-cos\theta}}\)
回転半径 Rg
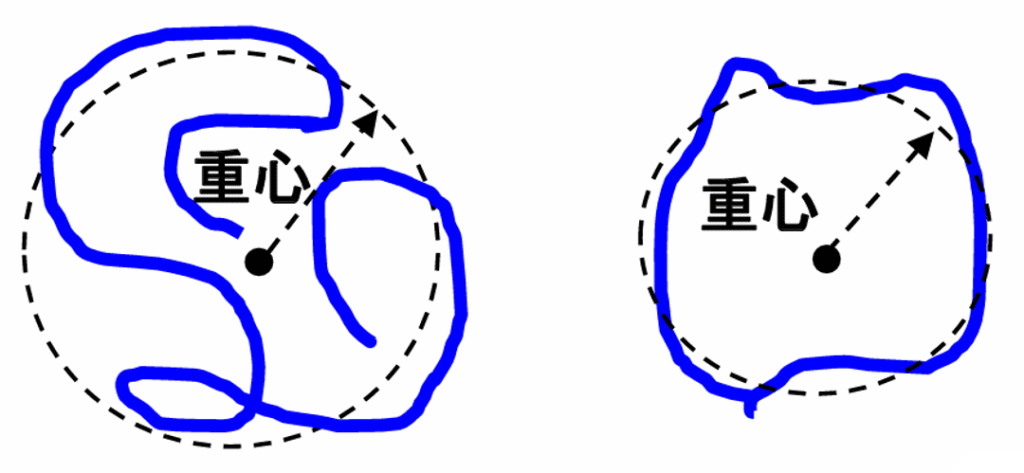
回転半径(radius of gyration, \(R_g\))は、高分子の質量分布の広がりを表す指標であり、重心からの平均距離に基づいて定義されます。
\(\Large{R_g^2 = \frac{1}{n} \sum_{i=1}^{n} (\mathbf{r}_i – \mathbf{r}_{\text{cm}})^2}\)
ここで、
- \(\mathbf{r}_i\) は i 番目のモノマーの位置、
- \(\mathbf{r}_{\text{cm}}\) は高分子の重心です。
(1) 理想鎖の場合
理想鎖モデルでは、回転半径と両末端間距離の間には次の関係があります。
\(\large{\langle R_g^2 \rangle = \frac{\langle R^2 \rangle}{6}}\)
すなわち、 \(\large{R_g = \frac{R}{\sqrt{6}}}\)
となります。つまり、両末端間距離と回転半径は比例関係にありますが、回転半径のほうが短くなります。
両末端間距離と回転半径の違い
| 指標 | 定義 | 代表的な値(理想鎖) |
|---|---|---|
| 両末端間距離 R | 高分子の両端の距離 | \(R \sim b \sqrt{n}\) |
| 回転半径 Rg | 高分子の重心からの平均距離 | \(R_g \sim \frac{R}{\sqrt{6}}\) |
- 両末端間距離 R は高分子の全体的な長さを表すのに適している。
- 回転半径 Rg は高分子の広がり(コンパクトさ)を示す。
- 高分子溶液の散乱実験(X線散乱や光散乱)では、Rg が測定されることが多い。
応用と物理的意味(参考)
高分子の溶液状態では、溶媒との相互作用によって高分子のサイズが変化します。
- 良溶媒(溶けやすい場合) → 高分子鎖は膨張し、Rg や R が大きくなる。
- θ溶媒(理想鎖と同じ振る舞い) → ガウス鎖モデルが成り立つ。
- 貧溶媒(溶けにくい場合) → 高分子鎖はコンパクトに縮む(グロビュール状態)。
この理由ですが、溶けやすい溶媒を使った場合、つまり、高分子が高分子同士でくっつくよりも溶媒とふれていたい場合は、高分子は表面積が大きくなるように広がるみたいなイメージを持つと分かりやすいです。
まとめ
- 両末端間距離 R は高分子鎖の端から端の距離。
- 回転半径 Rg は高分子の広がりの指標で、重心周りの分布を考慮。
- 理想鎖では \(R_g = R/\sqrt{6}\) の関係が成り立つ。
- 高分子の物性(粘度、散乱、膨潤など)は、主に \(R_g\) に影響を受ける。
このように、両末端間距離と回転半径は、高分子鎖のサイズや形状を定量的に理解するための重要なパラメータとなります。

コメント