核形成に伴う自由エネルギーの変化について解説！！【過冷却も】

相転移や結晶成長の初期段階では、新しい相（固相や液相など）の核が形成されます。このとき、系の自由エネルギーは体積エネルギーの減少と表面エネルギーの増加の影響を受けます。

これを表すのが、核形成に伴うギブス自由エネルギーの変化（ΔG）であり、核の半径 rに依存する関数です。

1. 自由エネルギーの変化の式

核の自由エネルギー変化 \(\Delta G\) は、以下の2つの項からなります。

1. 体積自由エネルギー変化（\(\Delta G_v\)）
   • 新しい相が形成されることにより得られるエネルギー（エネルギーの減少）。
   • 体積に比例し、負の値をとる。
2. 表面自由エネルギー変化（γ）
   • 界面ができることで発生するエネルギー（エネルギーの増加）。
   • 表面積に比例し、正の値をとる。

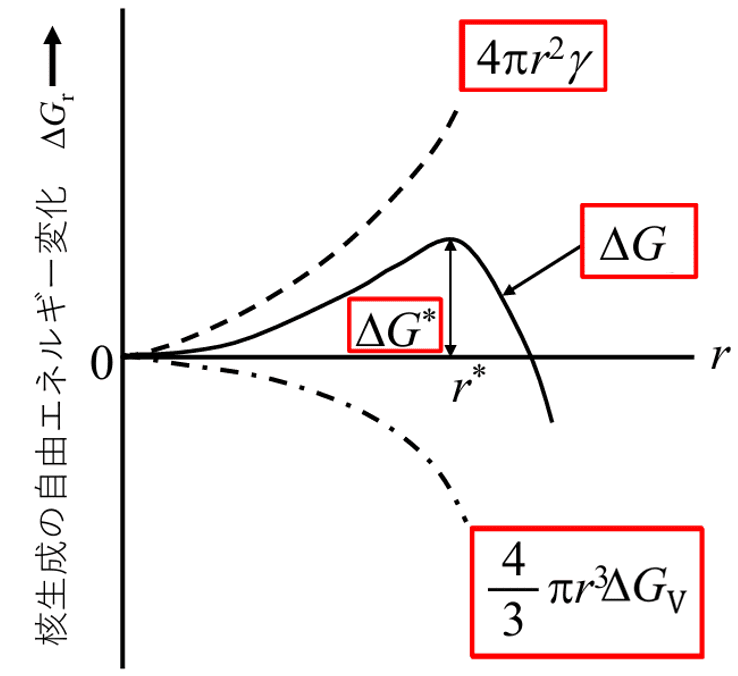
これを考慮すると、球状の核（半径 r）について、自由エネルギーの変化 \(\Delta G\) は次のようになります。

\(\Large{ΔG(r)=\Delta G (r) = \frac{4}{3} \pi r^3 \Delta G_v + 4\pi r^2 \gamma}\)

ここで、

• \(\Delta G_v\)：単位体積あたりの自由エネルギー変化（負の値）
• \(\gamma\)：界面張力（正の値）
• \(r\)：核の半径

2. 臨界半径 r^* と臨界自由エネルギー ΔG^∗

核の成長条件を考えると、自由エネルギーが最大になる 臨界半径 \(r^*\) を求めることが重要になります。

臨界半径を超えてしまえば、あとは核が大きくなるにつれて自由エネルギーが減少していくのでどんどん核が成長していくからです。

\(\Large{\frac{d\Delta G}{dr} = 0}\)

を解くと、臨界半径 \(r^*\) は

\(\Large{r^* = -\frac{2\gamma}{\Delta G_v}}\)

となります。この{r^*} より小さい核は消滅し、大きい核は成長するというわけですね。
また、対応する臨界自由エネルギー \(\Delta G^*\) は、

\(\Large{\Delta G^* = \frac{16 \pi \gamma^3}{3 (\Delta G_v)^2}}\)

となります。これは、核が成長するために越えなければならないエネルギー障壁です。

3. 過冷却と核形成

核が形成されるためには、\(\Delta G_v\)（体積自由エネルギー変化）が十分に大きくなる必要があります。
ここで、\(\Delta G_v\) は、温度 T に依存し、特に液体が過冷却状態にあるとき、核形成が進みやすくなります。

\(\Large{Delta G_v = \frac{\Delta H_f (T_m – T)}{T_m}}\)

ここで、

• \(\Delta H_f\)：凝固の潜熱（単位体積あたり）
• T_m：融点（平衡凝固温度）
• T：現在の温度

温度 Tが低くなるほど \(|\Delta G_v|\) が大きくなり、臨界半径 \(r^*\) が小さくなるため、核形成が起こりやすくなることが分かりますね。

４. まとめ

• 自由エネルギー変化は、体積自由エネルギーの減少と表面自由エネルギーの増加のバランスで決まる。
• 臨界半径 \(r^*\) を超えると核が成長し、小さいと消滅する。
• 温度が低くなる（過冷却が進む）と核形成が起こりやすくなる。