今回扱うのはアレニウス式です。
この式は、高校化学の教科書に発展として出てくるので、高校の時にちらっと見聞きしたことある人もいると思います。
まず初めに、アレニウスの式ってのはこんな式。
$$\Large{k = Ae^{-\frac{Ea}{RT}}}$$
kは反応速度定数。
さらに、Aは頻度因子、Eaは活性化エネルギー、Rは気体定数、Tは温度。
ここからは、アレニウスの式の意味とアレニウスプロットについて説明していきます!
アレニウスの式の意味
一般に温度が高くなると反応速度は速くなるんだけど、それを式にしたのがアレニウスの式。
だから、基本的には反応速度定数と温度の関係を見てる。
$$\Large{k = Ae^{-\frac{Ea}{RT}}}$$
ここで、Aの頻度因子は、分子の形などによる反応のしやすさを補正するもの。
確率項って名前がついてる。ただの定数だしあんまり注目しなくていい。
大事なのは\(e^{-\frac{Ea}{RT}}\)の部分。
実は\(RT\)が1モルあたりのエネルギーの単位になっているのは分かりますか?
これは、気体の状態方程式\(PV=nRT\)と、PVがエネルギーの単位であることから分かる。
活性化エネルギー\(Ea\)も\(RT\)もエネルギーの単位だから、
\(\large{e^{-\frac{Ea}{RT}}}\)の部分は、エネルギー項と呼ばれている!
このことは押さえておくべき。
- 温度と反応速度はの関係を表したのがアレニウスの式
- アレニウスの式は\(A\)(頻度因子)の確率項と\(e^{-\frac{Ea}{RT}}\)のエネルギー項に分けられる!
アレニウスプロット
アレニウスプロットとは?
これを説明する前にアレニウスの式を変形しておこう。
$$\Large{k = Ae^{-\frac{Ea}{RT}}}$$
両辺に自然対数をとって、\( \iff \)(lnをつけて)
$$\Large{logk = log{Ae^{-\frac{Ea}{RT}}}}$$
\(loge^x = x\)であることを使えば、
$$\Large{logk = log A -\frac{Ea}{RT}}$$
この式が今回のキーとなる式。
何がいいかっていうと、直線で表せること。
実際、\(log k\)を縦軸、\(\frac{1}{T}\)を横軸に取ると、
切片\(log A\)、傾き\(-\frac{Ea}{R}\)の直線になる!!!傾きの単位はケルビン(K)。
分かりにくければ、懐かしの一次関数\(y = ax + b\)を思い出して、
\(y\)を\(logk\)に、\(x\)を\(\frac{1}{T}\)に、\(a\)を\(\frac{Ea}{R}\)に\(b\)を\(log A\)に変えればいい。
アレニウスプロットを使った問題と解答解説
実際の試験ではこんな問題が出る。
問題
次のデータをもとに、アレニウスプロットを利用してEaとAを求めよ。
| \(T(K)\) | \(k(cm^3 mol^{-1}s^{-1})\) |
|---|---|
| 298 | \(1.11×10^{-13}\) |
| 311 | \(1.30×10^{-13}\) |
| 331 | \(1.55×10^{-13}\) |
| 343 | \(1.71×10^{-13}\) |
解答
まず、アレニウスプロットをするために与えられたデータを元に座標を求める。
| \(log k\) | \(\frac{1}{T}\) |
|---|---|
| -29.8292 | 0.003356 |
| -29.6412 | 0.003215 |
| -29.4754 | 0.003021 |
| -29.3971 | 0.002915 |
これを座標に打っていくと、下の図のようになる。
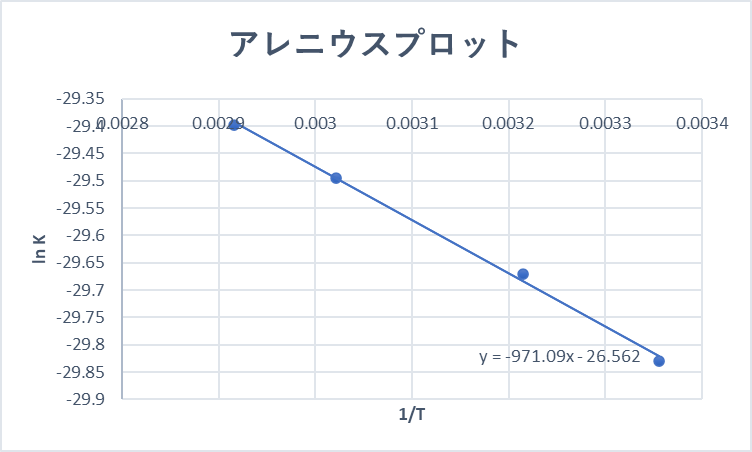
グラフより、傾き\(-\frac{Ea}{R}\)は-971.09
切片\(log k\)は-26.562
よって、
\(Ea = 971.09 \times 8.314 \simeq 8073[J mol_{-1}]\)
\(A = e^{26.562} 2.91 \simeq \times 10_{-12}(cm^3 mol^{-1}s^{-1})\)
これが答えだ!!!
ちなみにAの単位が速度定数と同じになっている。

コメント