この記事では、動径波動関数や動径分布関数の違いはもちろん、さらに無機化学のレポートや試験でみる、動径波動関数や動径分布関数のグラフから、どのグラフがどの軌道を表すものなのかを答える問題の、その解答方法を書いています!
はじめに
動径波動関数と動径分布関数を軽くおさらいしておきます。
動径波動関数 R(r)
電子の状態を表す波動関数がありますが、波動関数は動径部分の関数と角部分の関数の積として表すことが出来ます。
そのうち波動関数の動径部分を表す関数が、動径波動関数 R(r) です。
動径分布関数 P(r)
動径分布関数P(r)は式で表すと動径波動関数R(r)と半径rを使って、下式のように表すことが出来ます。
\(\Large{P(r) = R(r)^2×r^2}\)
半径rで厚さdrの球殻内のどこかに電子を見出す確率は、P(r)にdrをかければ求まります。
グラフ問題の解き方
ポイント1:動径節の数を求める
動径節とは、動径波動関数のグラフが0を通過する点(単に0である点でないことに注意)のことです。
動径節の数は主量子数nと方位量子数lから求めることが出来ます!
(動径節の数)= \(\Large{n – l – 1}\)
例えば、2s軌道はn=2、l=0なので、動径節を1つ持っています。
ポイント2:s軌道以外のすべての軌道は、原子核の位置で存在確率がゼロになる
これから、動径波動関数と動径分布関数の両方のグラフにおいて、核の位置(r=0)でゼロになるようなグラフがあれば、それはs軌道のグラフだと知ることが出来ます。
ポイント3:主量子数が大きいほど、原子核から遠くに電子が居る
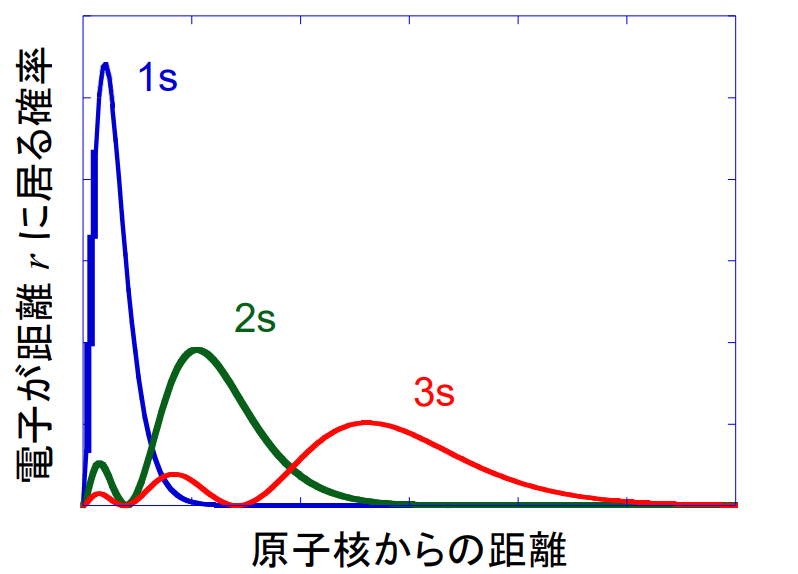
下図はs軌道それぞれの原子核からの距離rと、電子が距離rに存在する確率を表したものです。
主量子数nが大きくなると軌道は広がっていくので、原子核から離れたところに電子がいやすくなります。
練習問題
最後に練習問題を解いて確認しておきましょう!
問題
次の図は、H原子の1s, 2s, 2p原子軌道の動径分布関数を示したものである。(縦軸:R(r), 横軸:半径r)
それぞれどの軌道を示しているかを答えよ。
解答と解説
青:1s軌道
赤:2s軌道
緑:2p軌道
考え方の1例を示しておきます。
まず、動径節の数の公式:n-l-1を使って1s、2p軌道が0個、2s軌道が1個であることを先に求めておきます。
次に、原子核の近くに電子がいる確率が高い青のグラフが主量子数1の1s軌道だと分かります。
そして、原点(r=0)以外で0をとる点がある赤いグラフが、唯一動径節が1つある2s軌道だと分かり、残った緑の軌道が2p軌道だと分かります。
これですべての軌道が分かりました!


コメント