今回は無機化学の錯体の分野で登場する結晶場理論を丁寧に解説していきます!
結晶場理論とは?
結晶場理論は、錯体について考える時に登場する考え方の一つです。
配位子の孤立電子対を負の点電荷としてとらえ、中心金属イオンのd軌道の電子との反発を考えます。
電子同士の距離が近かったら反発のせいで不安定化するし、逆に遠かったら安定化する…みたいな感じです。
ちなみに、これは割と大雑把な考え方なので、もっとちゃんと考える時は配位子場理論というもう一つの考え方を使うことになります。

結晶場理論の具体例
ここからは、具体的に何を考えているのかを八面体錯体の例を使って説明していきたいと思います。
八面体錯体
正八面体錯体は、下の図のような形をしています。
金属イオンであるMn+イオンを中心に、赤色の6つの配位子が配位していますね。
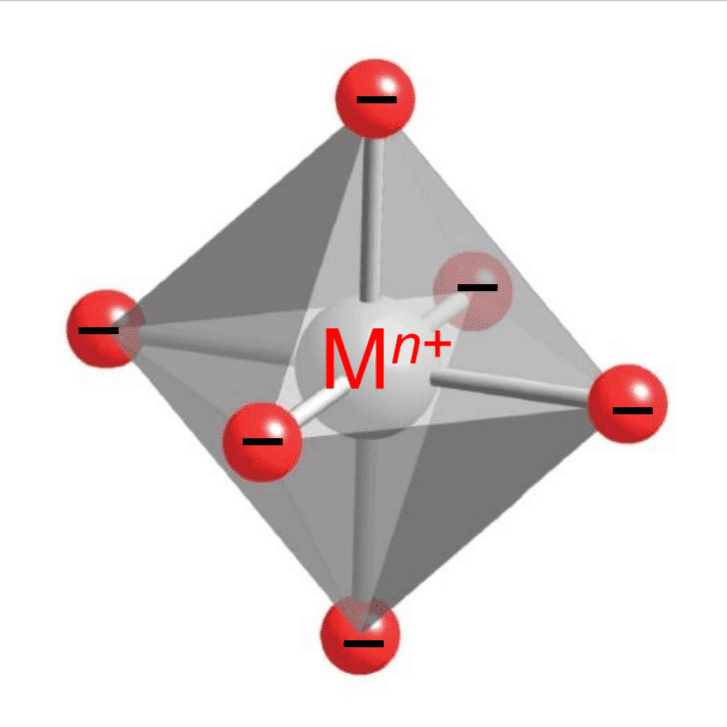
結晶場理論は配位子電子と金属d電子の反発を考えるので、
これと、d電子がどのように相互作用するかを考えればいいですね。
というわけで次にd電子について考えると、
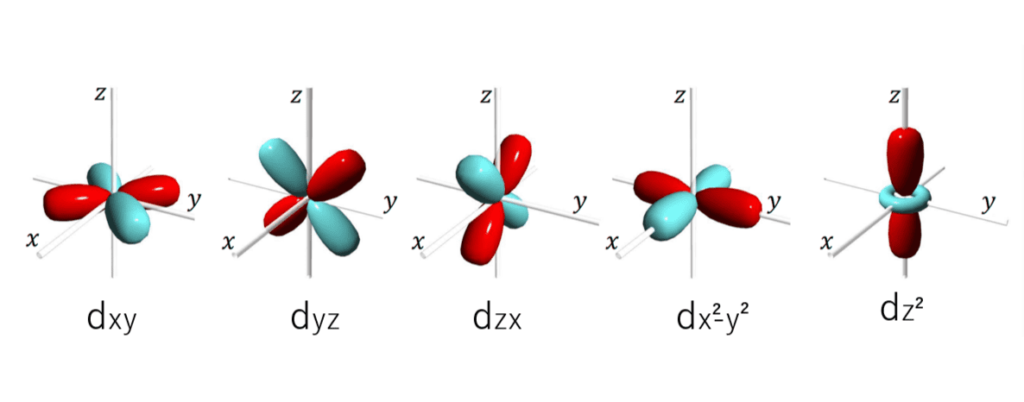
これら5種類が考えられます。
さて、どのd軌道がより強い反発を配位子電子から受けるか分かりますか?
…答えはdx2-y2と、dz2軌道です。
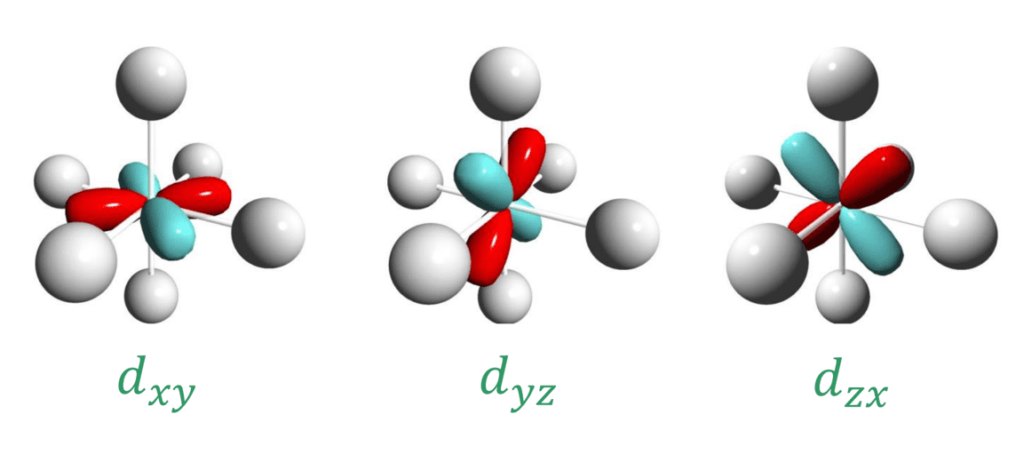
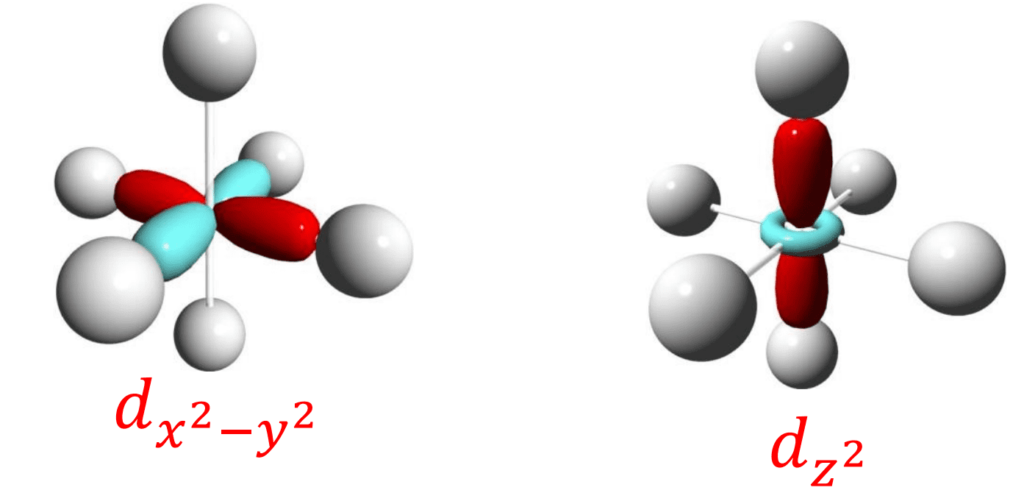
この図から、確かに”dx2-y2“と”dz2“軌道が強い反発を受けて不安定化することが分かりますね。
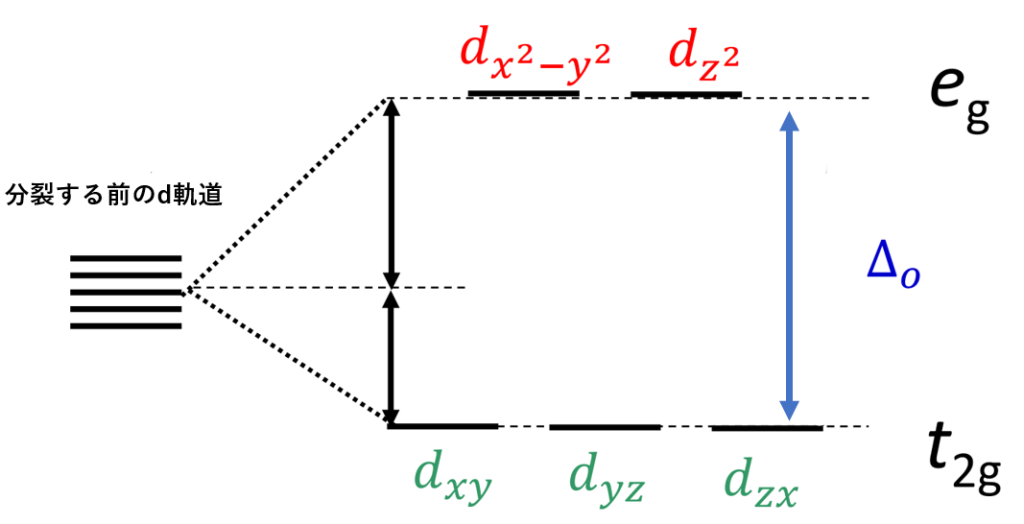
よって、それぞれの軌道のエネルギーは、2つに分かれます。
“dx2-y2“と”dz2“軌道がエネルギーが高く、”dxy” “dyz” “dzx“の3つの軌道がエネルギーが低くなります。
また、”dx2-y2“と”dz2“軌道をeg軌道、”dxy” “dyz” “dzx“の3つの軌道をt2g軌道と呼びます。これは今後すごく出てくるので絶対覚えた方がいいです。
また、それによってできた軌道のエネルギーの差を配位子場分裂パラメーター(Δo)といいます。
配位子場分裂パラメーターの大きさは錯体それぞれで違っていて、錯体の配位構造や配位子の種類、金属イオンの種類と酸化数によって変わってきます。
重心則について
ここで、重心則というものに触れておきましょう。
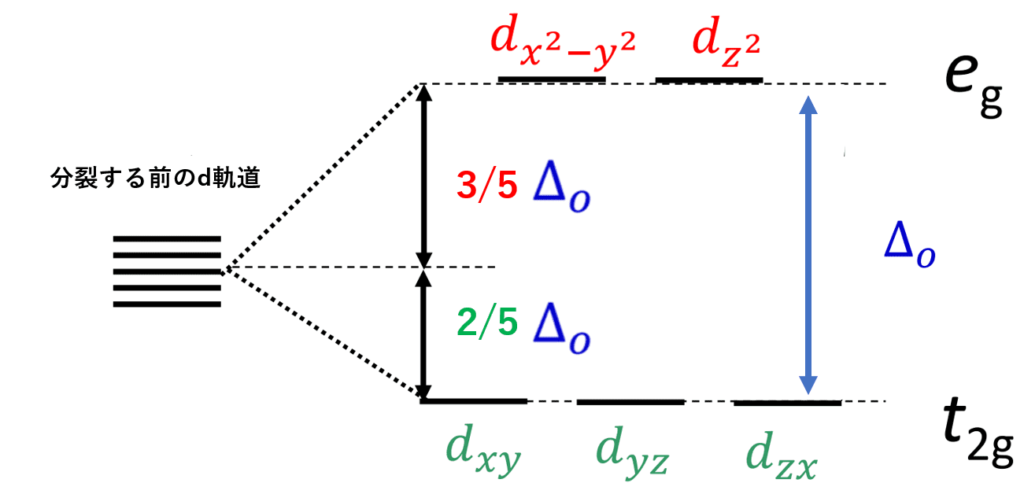
別に難しい話ではなく、重心則とは分裂後の5つの軌道のエネルギーをすべて足すと、分裂する前の軌道のエネルギーになるよってことです。
これを使えば、“dx2-y2“と”dz2“軌道は重心より3/5Δoだけ高く、“dxy” “dyz” “dzx“の3つの軌道は重心より2/5Δoだけ低くなることが分かります。これは結構重要です!
配位子場安定化エネルギー(LFSE)について
配位子場分裂パラメーターを学習することで、配位子場安定化エネルギー(LFSE)を理解できるようになります。
概要
配位子場安定化エネルギー(LFSE)は軌道がどれだけ安定化しているかを表したものです。
LFSEは、「配位子場分裂による安定化」と「スピン対生成による不安定化」の相対的な大きさを反映してきまる値で、後々やる軌道のスピンを予測するのに必要になってくる値です。
配位子場分裂パラメーターとスピン対生成エネルギー(P)の二つの値が必要になります。
具体例その1(d2とd8)
今回は、d軌道に電子が2個入っているd2電子配置と、電子が8個入っているd8電子配置について考えていきます。
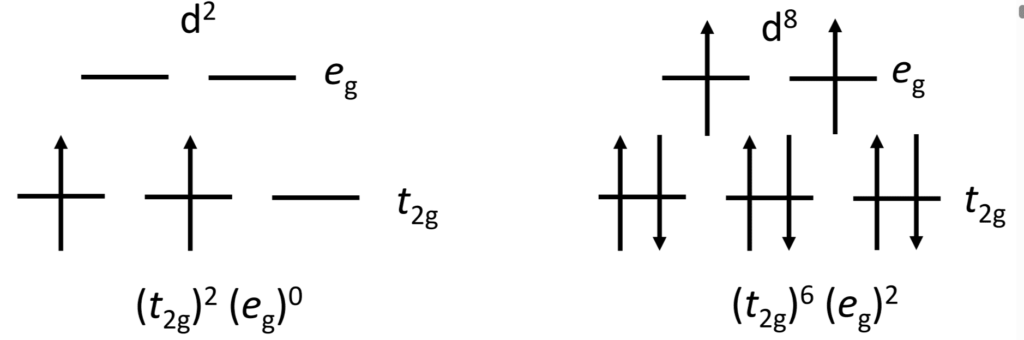
始めにd2電子配置の配位子場安定化エネルギー(LFSE)を求めていきます。
2つの電子はよりエネルギーの低いt2g軌道に入るので、上図のような電子配置になりますよね。
重心則よりt2g軌道は分裂前の軌道より(2/5)Δoだけエネルギーが低かったので、その軌道に電子2つが入るd2電子配置のLFSEは、
\(\Large{2 \times -\frac{2}{5}\Delta_o = -0.8\Delta_o} \)
となります。安定化するのでLFSEは負の値です。
次はd8です。
今回はeg軌道に2つ、t2g軌道に6つ電子が入るので、配位子場分裂による寄与は、
\(\Large{2 \times \frac{3}{5}\Delta_o + 6 \times -\frac{2}{5}\Delta_o = -1.2\Delta_o} \)
となります。
また、d8電子配置のスピン対の数は3つで、分裂前の軌道のスピン対の数も3つなので、今回はスピン対生成による寄与は考えなくていいです。
したがって、LFSE = \( -1.2\Delta_o \)
となります。
具体例その2(d4)
では、d4電子配置はどうでしょうか? 実は、2通りの電子配置が考えられます。
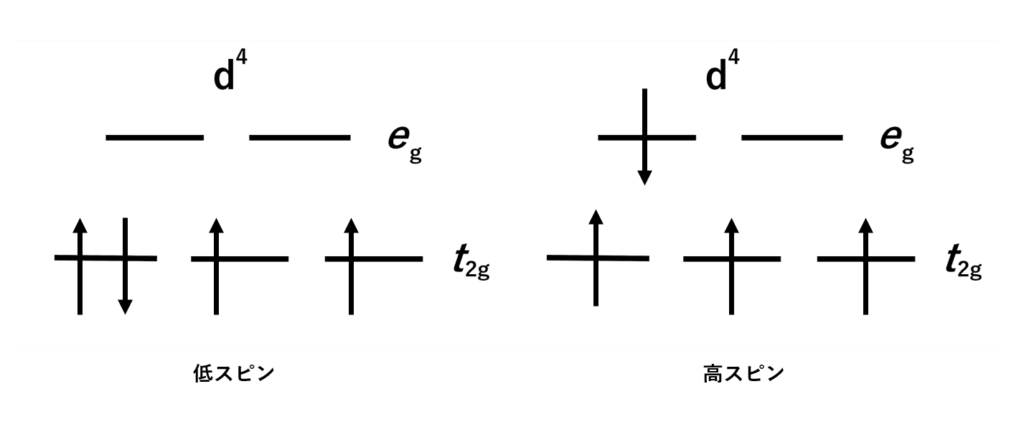
全ての電子がt2g軌道に入っている低スピン状態と、スピン対生成を避けるために一部の電子が先にeg軌道に入る高スピン状態の2通りです。
それぞれの配位子場安定化エネルギーを見てみると、
低スピンが、\(4 \times -\frac{2}{5}\Delta_o + P = -1.6\Delta_o + P\)
※ここでPはスピン対生成エネルギーです。分裂前の軌道ではスピン対がゼロだったのに対し、低スピン状態ではスピン対が1つ増えています。
高スピンが、\(3 \times -\frac{2}{5}\Delta_o + 1 \times \frac{3}{5}\Delta_o = -0.6\Delta_o )\
となります。
ではどちらの配置が有利でしょうか?
それは配位子場分裂パラメーター(Δo)とスピン対生成エネルギー(P)に大小関係によってきまります。
その大小関係を決める手掛かりになるのが、次に解説する「弱配位子場と強配位子場」です。
弱配位子場と強配位子場
弱配位子場はΔoが小さい配位子場で、強配位子場はΔoが大きい配位子場です。
下の図を見ると分かりやすいと思います。
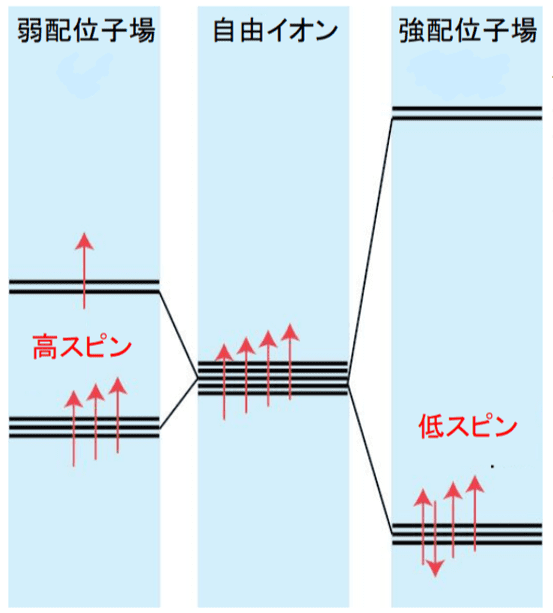
図より、強配位子場の方が軌道の安定化による寄与が大きいことがわかります。
だから、強配位子場はたとえスピン対を作って多少不安定化しても、低スピンを好みます。
逆に弱配位子場は軌道の安定化による寄与が小さくスピン対生成エネルギーが相対的に大きくなるので、高スピンを好みます。
配位子場の強さは「分光化学系列」という配位子を並べた順番で大体わかります。
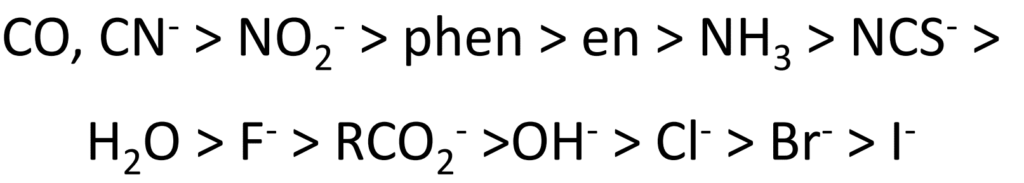
COやCN–は強配位子場配位子で、逆にI–は弱配位子場配位子です。
今回はこれで終わります。お疲れさまでした!!

コメント