【大学化学】波動関数とシュレーディンガー方程式とは？超わかりやすく解説！

「量子化学って難しそう…」「波動関数やシュレーディンガー方程式がよくわからない…」

大学で化学を学び始めると、多くの人が量子化学の抽象的な概念に戸惑うかもしれません。しかし、波動関数 (wave function) とシュレーディンガー方程式 (Schrödinger equation) は、ミクロな世界の原子や電子のふるまいを理解し、ひいては化学結合や分子の性質、化学反応を根本から理解するための非常に重要なツールなんです。

この記事では、数式だらけの難しい話は一旦脇に置いて、

• 波動関数って、結局なんなの？
• シュレーディンガー方程式が教えてくれることって？
• これらが化学現象の理解にどう繋がるの？

といった疑問に、初心者にも分かりやすくお答えします。この記事を読めば、量子化学の入り口が少し身近に感じられるはずです！

---

波動関数 (Ψ) ってなに？～電子の「住所録」みたいなもの～

すごくざっくり言うと、波動関数 (記号：\(\Psi\) ) は、原子や分子の中にいる電子の「状態」を表す情報が詰まった関数です。

古典的な物理学では、物体の位置や運動量はピタッと決まりますよね？ でも、ミクロな世界の電子は、粒子としての性質と波としての性質を併せ持つため、特定の位置に「いる」とは言えません。「この辺りにいそうだな」という確率でしか存在を記述できないのです。

波動関数そのものに直接的な物理的意味はありませんが、波動関数の2乗 (\(\Psi^2\)) は、ある場所で電子が見つかる確率（存在確率密度） を表します。つまり、波動関数が分かれば、電子が原子核の周りのどの辺りにどれくらいの確率で存在するのかが分かる、というわけです。

波動関数のポイント

• 電子の波としての性質を表す: 電子は波のように振る舞うため、その状態を波の関数で記述します。
• 直接的な意味はないが、2乗すると存在確率になる: \(\Psi^2\) が大きい場所ほど、電子が見つかる可能性が高いです。
• 電子のエネルギーや軌道の形も決める: 後述するシュレーディンガー方程式を解くことで得られる波動関数には、電子のエネルギーや、いわゆる「電子雲」の形（原子軌道や分子軌道）の情報も含まれています。

イメージで捉えよう！

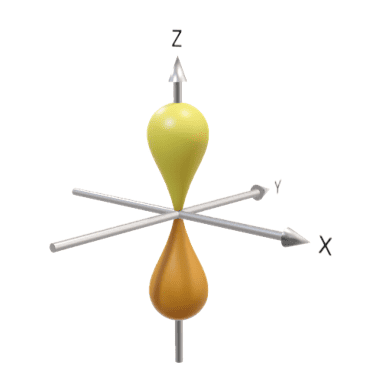
例えば、水素原子中の電子の波動関数が分かると、「電子は原子核からこのくらいの距離に、こんな形の雲みたいに広がって存在している可能性が高いぞ」というイメージが掴めます。これが、高校化学で習うs軌道、p軌道といった原子軌道の正体です。

---

s軌道とp軌道の３D模式図を挿入しておきます。

シュレーディンガー方程式ってなに？～波動関数を求めるための「レシピ」～

では、その重要な波動関数はどうやって求められるのでしょうか？ それを教えてくれるのが、シュレーディンガー方程式です。

シュレーディンガー方程式は、量子化学における最も基本的な方程式の一つで、原子や分子のエネルギーや波動関数を計算するための方程式です。すごく簡単に言うと、「この条件（ポテンシャルエネルギー）の下で、電子はどんな波動関数（状態）をとるの？」という問いに答えるための「レシピ」 のようなものです。

シュレーディンガー方程式の役割

• 波動関数 (\(\Psi\)) を求める: この方程式を解くことで、特定の原子や分子中の電子の波動関数が具体的に得られます。
• エネルギー固有値を求める: 波動関数と同時に、その電子が持つことができる特定のエネルギーの値（これをエネルギー固有値といいます）も求まります。電子はどんなエネルギーでも取れるわけではなく、とびとびの決まったエネルギー準位しか取れない、という量子化の概念がここから出てきます。

方程式の形（イメージ）

詳細な数式はここでは扱いませんが、シュレーディンガー方程式は一般的に以下のような構造をしています。

(ある演算子) \(\Psi\) = (エネルギー) \(\Psi\)

左辺の「ある演算子」はハミルトニアン演算子と呼ばれ、系の全エネルギー（運動エネルギーとポテンシャルエネルギーの和）を表します。この方程式は、「ハミルトニアン演算子を波動関数に作用させると、その波動関数自身にエネルギーを掛けたものと等しくなる」ということを意味しており、このような関係を満たす波動関数 \(\Psi\) とエネルギー E を見つけ出すのが、シュレーディンガー方程式を「解く」ということです。

---

なんとなくのイメージを持ってもらうため、イメージ図を作りました。

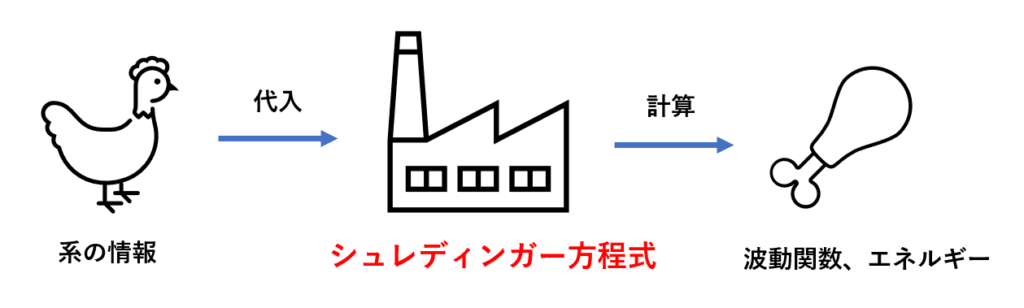
系の情報（全ポテンシャルエネルギー）をシュレディンガー方程式に代入することで、波動関数やエネルギーが求まるって感じです。

波動関数とシュレーディンガー方程式が化学現象の理解にどう役立つのか？

これら量子化学の基本概念が、具体的にどのように化学現象の理解に繋がるのでしょうか？

1. 原子・分子の構造の理解 (原子軌道・分子軌道) 🛰️ シュレーディンガー方程式を解いて得られる波動関数は、電子の空間的な広がり、つまり原子軌道（s軌道、p軌道、d軌道など）や、原子同士が結合して分子を形成する際の分子軌道の形やエネルギーを教えてくれます。これにより、なぜ特定の形の分子が安定に存在するのか、結合の強さや方向性はどう決まるのか、といった原子・分子レベルでの構造を理論的に説明できます。
2. 化学結合の本質の理解 🤝 例えば、二つの原子が近づいて共有結合を形成する際、それぞれの原子の原子軌道が重なり合って新しい分子軌道ができます。この分子軌道を電子が占有することで、原子単独でいるよりもエネルギー的に安定になるため結合が形成されます。波動関数を用いることで、このような結合形成のメカニズムや結合エネルギーを定量的に評価できます。
3. 分子のスペクトルの説明 🌈 分子が光を吸収したり放出したりする際、電子は異なるエネルギー準位間を遷移します。シュレーディンガー方程式から得られるエネルギー準位の情報は、分子がどのような波長の光を吸収・放出するのか（つまり、分子のスペクトル）を予測・説明するのに役立ちます。これは、物質の同定や構造決定に不可欠な分光分析の理論的基礎となります。
4. 化学反応の予測と解析 🧪 反応物から生成物へと変化する化学反応の経路や、反応の起こりやすさ（活性化エネルギーなど）を理論的に見積もる際にも、量子化学計算が活用されます。分子の構造や電子状態を波動関数に基づいて詳細に調べることで、より効率的な反応経路の設計や、新しい触媒の開発などに繋がります。

よくある質問（Q&A）

---

まとめ

今回は、量子化学の基本的な概念である波動関数とシュレーディンガー方程式について、その意味と化学現象への繋がりを中心に解説しました。

• 波動関数 (Psi): 電子の状態を表す関数で、2乗すると電子の存在確率を示す。原子軌道や分子軌道の形、エネルギーの情報も含む。
• シュレーディンガー方程式: 波動関数と、電子が取りうるエネルギー準位を求めるための方程式。
• 化学への貢献: 原子・分子の構造、化学結合、スペクトル、化学反応など、様々な化学現象をミクロな視点から理論的に理解するための基礎となる。

数学的な扱いは確かに複雑ですが、これらの概念が「何を表していて、何が分かるのか」という本質的な部分を掴むことが、量子化学アレルギーを克服する第一歩です。この知識が、皆さんの化学の学びをより深く、面白いものにする手助けとなれば幸いです！

（参考）もっと詳しく知りたい人へ 📚

この記事で、波動関数とシュレーディンガー方程式の基本的な考え方に触れていただけたでしょうか？もし、さらに量子化学の世界を探求したいと思ったら、以下のような方法で学習を深めていくのがおすすめです。

より網羅的で詳しい解説は、専門の教科書で学ぶのが近道です。ここでは、比較的初学者にも取り組みやすいと評判の教科書をいくつか紹介します。ご自身のレベルや興味に合わせて選んでみてください。

• マッカーリ・サイモン 物理化学 : 少し分厚いですが、丁寧な説明と豊富な例題で、多くの大学で教科書として採用されています。量子化学の章は特におすすめです。
• アトキンス 物理化学 : こちらも定番の教科書で、図やイラストが多く、視覚的にも理解しやすい工夫がされています。
• ザボ・オストランド 新しい量子化学 : より本格的に量子化学計算の理論を学びたい人向けの、少し専門的な教科書です。

(注: 上記は一般的な例です。実際に書店で手に取ってみて、自分に合うものを選ぶのが一番です。また、大学の先生や先輩におすすめを聞いてみるのも良いでしょう。)