本記事では、複合材料のヤング率の求め方や影響因子について解説します。
1. 複合材料のヤング率の計算方法
複合材料のヤング率は、主に材料の配置(並列モデル・直列モデル)によって異なります。
基本的に2つのモデルのみを扱うので、以下で紹介する2つを理解出来たら完璧です!
(1) 並列モデル(Voigt モデル)
このモデルは、ファイバーの方向に荷重が作用する場合に適用されます。
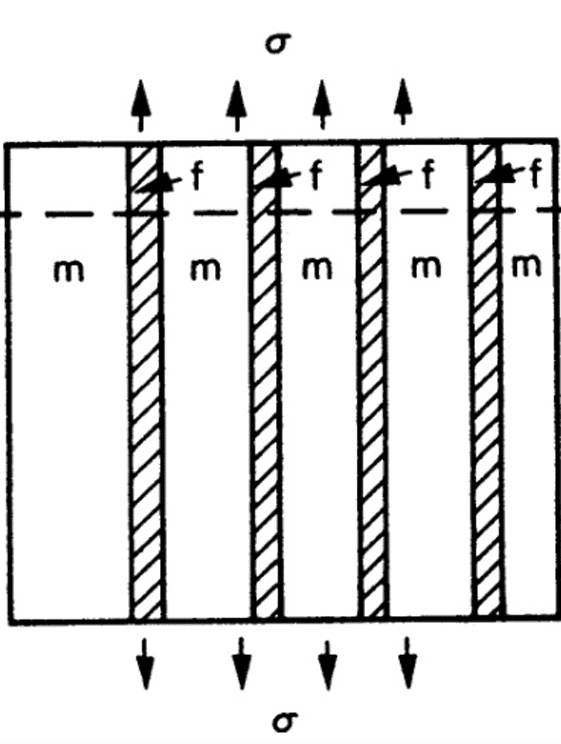
並列モデルのヤング率の式
並列配置の複合材料では、荷重がすべての成分に均等にかかるため、ヤング率は以下の式で求められます。
\(\Large{E_c = V_f E_f + V_m E_m}\)
ここで、
- \(E_c\) :複合材料全体のヤング率
- \(E_f\) :強化材(ファイバーなど)のヤング率
- \(E_m\) :母材(マトリックス)のヤング率
- \(V_f\) :強化材の体積分率
- \(V_m\) :母材の体積分率(\(V_m = 1 – V_f\))
並列モデルでの式の導出
応力σは全部の和で、ひずみεは成分ごとに同じであるため、体積分率を考慮して、
$$\large{
\begin{aligned}
\sigma &= V_f \sigma_f + V_m \sigma_m \\
&= E_f V_f \varepsilon + E_m V_m\varepsilon
\end{aligned}
}$$
\(\varepsilon\) を消去すると、
\(\large{E_c =\frac{\sigma}{\varepsilon} = V_f E_f + V_m E_m}\)
(2) 直列モデル(Reuss モデル)
このモデルは、荷重がファイバーに対して垂直方向に作用する場合に適用されます。
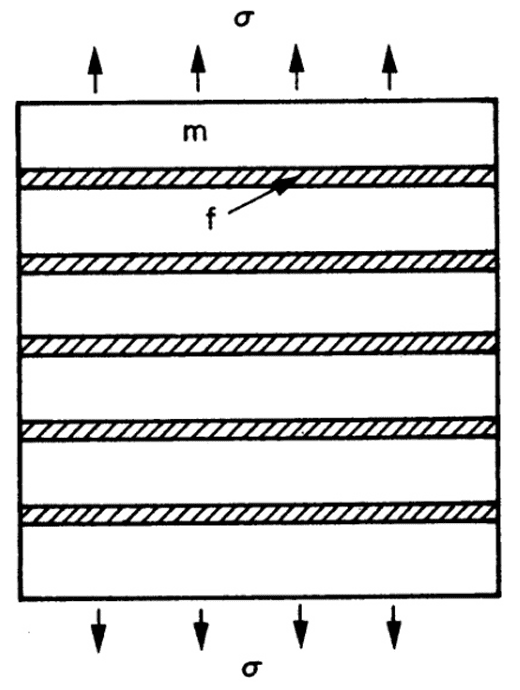
直列モデルのヤング率の式
直列配置の複合材料では、応力が均等で、ひずみが異なるため、ヤング率は以下の式で求められます。
\(\Large{\frac{1}{E_c} = \frac{V_f}{E_f} + \frac{V_m}{E_m}}\)
直列モデルでの式の導出
応力はすべての成分で等しいと考えられるので、 \(\large{\sigma = E_f \varepsilon_f = E_m \varepsilon_m}\)
ひずみの和が全体のひずみだから、体積分率を考慮すると、 \(\large{\varepsilon = V_f \varepsilon_f + V_m \varepsilon_m}\)
これをヤング率の定義 \(\large{E_c = \frac{\sigma}{\varepsilon}}\) に代入すると、
\(\large{\frac{1}{E_c} = \frac{V_f}{E_f} + \frac{V_m}{E_m}}\)
2. 複合材料のヤング率に影響を与える要因
(1) 材料の種類と性質
- 強化材(カーボンファイバー、ガラス繊維、ケブラーなど)のヤング率が高いほど、全体の剛性が向上します。
- 母材(ポリマー、金属、セラミックスなど)のヤング率も重要です。
(2) 体積分率(Vf)
- 強化材の割合が増えると、一般的にヤング率は高くなります。
- ただし、母材と強化材の界面接着が悪いと、期待された剛性を得られないことがあります。
(3) 繊維配向
- 一方向に配向した繊維では、並列モデルに近い挙動を示し、高いヤング率を持ちます。
- 無秩序に配向した繊維(ランダム配向)では、等方性の性質を持ち、ヤング率は中間的な値になります。
(4) 温度・環境条件
- 高温では母材(特にポリマー)が軟化し、ヤング率が低下します。
- 湿度の影響で母材が膨張すると、界面剥離が起こり、剛性が低下することがあります。
3. 実際の複合材料のヤング率の例
| 材料 | ヤング率(GPa) |
|---|---|
| 炭素繊維強化プラスチック(CFRP) | 100~300 |
| ガラス繊維強化プラスチック(GFRP) | 30~50 |
| ケブラー繊維強化プラスチック(AFRP) | 50~100 |
| 金属マトリックス複合材料(MMC) | 100~500 |
CFRP(炭素繊維強化プラスチック)は非常に高いヤング率を持ち、航空機やレーシングカーなどの分野で広く使用されています。
4. まとめ
- 複合材料のヤング率は、母材と強化材のヤング率、およびその体積分率によって決まる。
- 並列モデル(Voigt モデル)と直列モデル(Reuss モデル)を用いて理論的に算出可能。
- 材料の種類、配向、環境条件などがヤング率に大きく影響を与える。
複合材料を設計する際は、用途に応じたヤング率の調整が重要になります。各種計算モデルを適用しながら、適切な材料選定を行うことが求められます。

コメント