大学で無機化学を学んでいくと、分子の対称性について学ぶ機会があります。
これが結構大事で、なぜなら分子軌道の組み立てや分子振動の解析に対称の考え方は不可欠だからです。
対称性の系統的に取り扱うにあたって群論(group theory)と呼ばれる数学の考え方が便利なのですが、それを化学に応用する上で、タイトルにもあった対称操作が元になってきます。
それでは前置きが長くなりましたが、全部で5種類ある対称操作を一つずつ解説していきます!
対称操作とは?
対称操作とは、ある分子が全く同じ形に見えるように動かす操作です。
\(\ce{H2O}\)を例にとってみます。下の図を見てください。
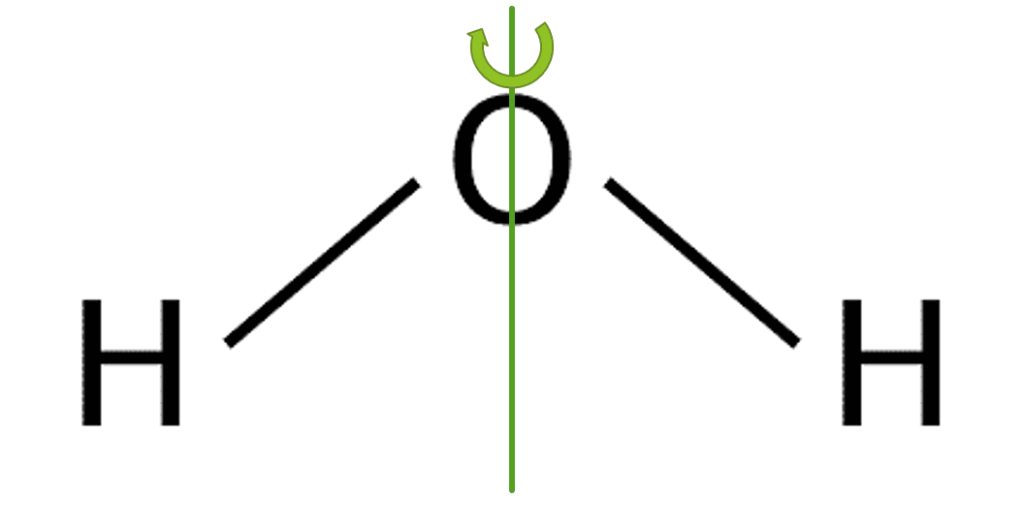
図のように、緑の軸を中心に、H2Oを180度だけ回転させた後と、回転させる前では、2つのH原子(H原子どうしは区別しません)と1つのO原子の位置が全く変わっていないことが分かると思います。
実際に、回転させる前と後の2枚の絵を誰かに見せたとしても、絵を見せられた人は2枚の絵が全く同じに見えますよね。
このことから、H2Oにとって「O原子を中心に180度回転させる」という操作は対称操作にあたることが分かります。
次は、対称操作の種類について説明していきます。
| 操作名 | 対象操作 | 対象要素 | 記号 |
|---|---|---|---|
| 恒等 | 恒等(何もしない) | 全空間 | E |
| 回転 | 360°/n だけ回転する | n回回転軸 | Cn |
| 鏡映 | 鏡像をつくる | 鏡移面 | σ |
| 反転 | 反転させる | 反転中心 | i |
| 回映 | 「回転」+「鏡像」 | n回回転軸 | Sn |
対称操作の解説
恒等 ’E’
一つ目は恒等です。
これは、「何もしない」という操作です。
ある分子に対して「何もしない」という操作をとったところで、その分子に変化はありませんよね。ちょっとややこしいですが。
とりあえず、「恒等操作は全ての分子がもつ」と覚えておいてください。
回転 ’Cn’
2つ目は回転です。
勘の良い人は気づいたかもしれませんが、先ほどH2Oを使って考えた例が回転に当たります。
\(\Large{\frac{360°}{n}}\)だけ回転したとき、分子が同じ形をしているとき、n回回転といいます。
さっきのH2Oの例は180°なので、n=2で2回回転ですね。
回転軸を120°回転させる場合は3回回転、90°なら4回回転になります。
回転軸と主軸
回転の操作をするとき、回転させる軸を回転軸といいます。
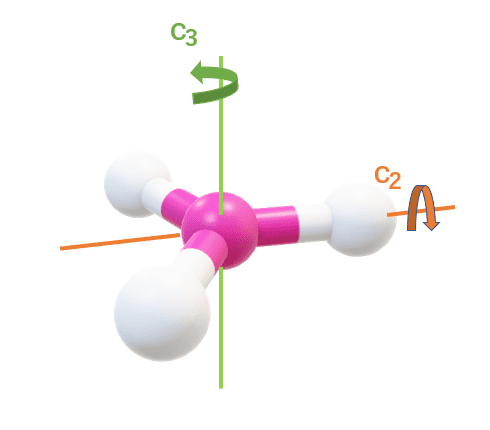
上の図は、NH3の立体モデルです。
これを見ると、C3とC2の二つの回転軸があることが分かります。
ここで、回転軸のうち、最も次数の高い、すなわち最もnが大きい回転軸を主軸といいます。
今回は3>2だから、C3のほうが主軸です。
また、立体的に考えるときは、主軸をz軸として考えます。
鏡映 ’σ’
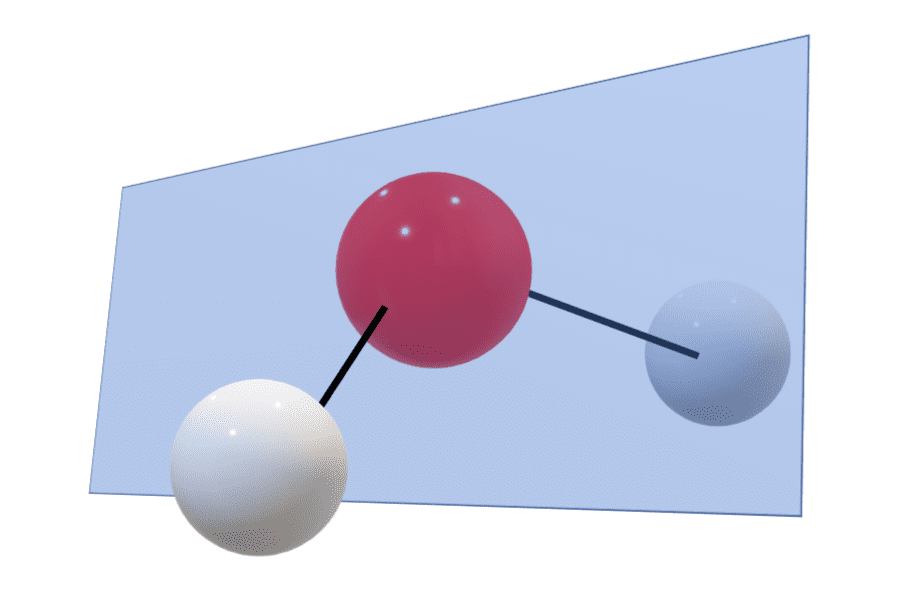
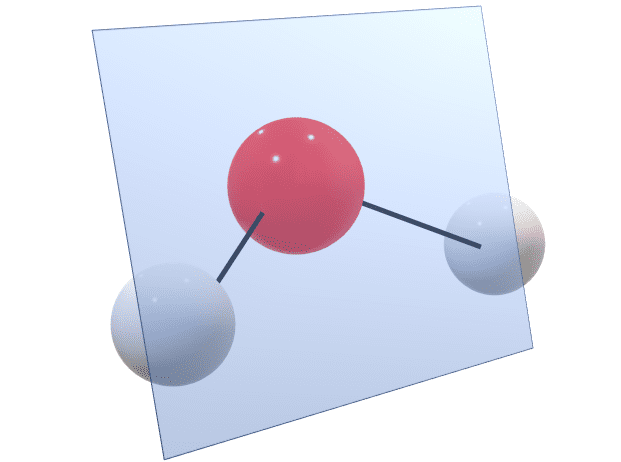
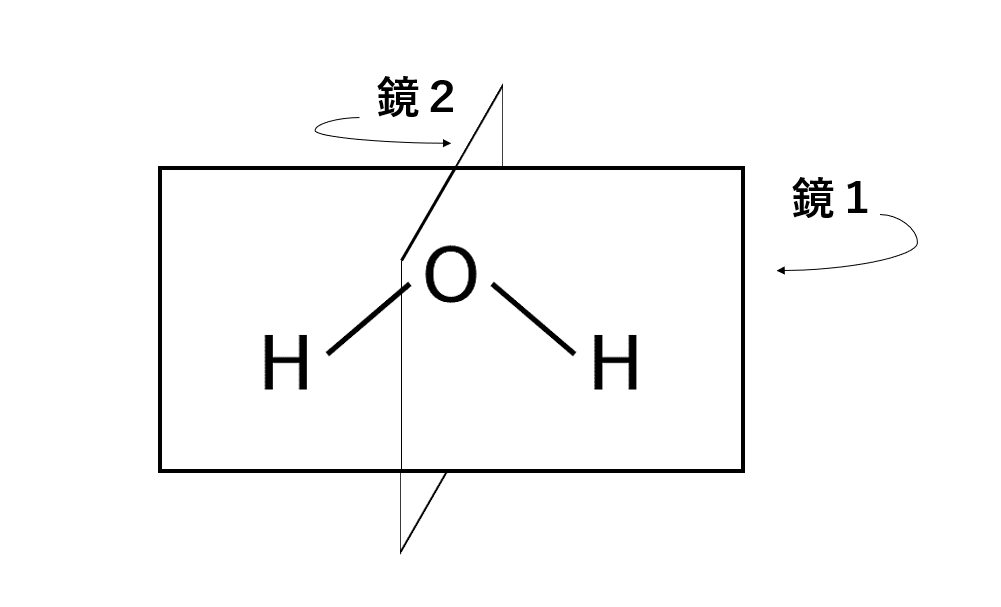
ある平面で鏡像を作る操作を鏡映操作といいます。H2Oの場合、二種類の鏡映操作が考えられます。
だいぶ分かりにくいですが、上の図はそのイメージ図です。
青い平面のやつが鏡だと思ってください。するとH2Oの半分が鏡に映りますがこれは元の状態のH2Oとまったく同じですよね。
鏡像面の種類
鏡像面が主軸を含むとき、σv(vertical)
鏡像面が主軸と直角になるとき、σh(horizontal)となります。
さらに鏡像面が、「主軸に直交する他の回転軸」が作る二面角を二等分し、自身も主軸を含む鏡面であるとき、σdとなります。
直角なのにhorizontal(水平)だったり、すこしややこしいです。
反転 ’i ’
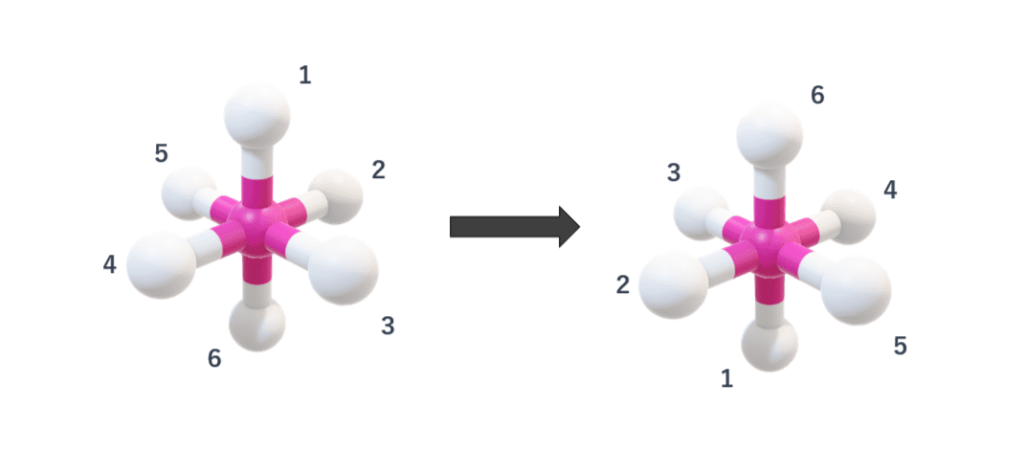
分子の中心を反転の中心として、全ての原子を反転させます。
例えば、(x, y, z)にある原子は、(-x, -y, -z)に移ります。
回映 ’Sn’
これが最後の対象操作です。
この操作は、回転と鏡映を組み合わせたようなイメージで、「n回回転軸で回転させ」、その後に「回転軸に垂直な面で鏡映操作をする」という二つの操作でできています。
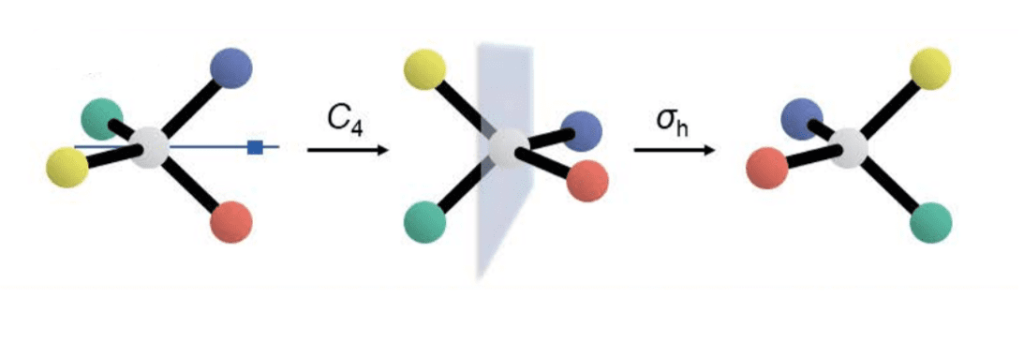
これで対称操作は終わりです。
お疲れ様でした!

コメント