今回は物理化学で扱う、ジュール・トムソンの実験を考えていきたいと思います。
正直、この実験はあんまり有名ではありません。
しかし、この実験で得られた「ジュール・トムソン効果」は、実は日常生活で大活躍しています。
何に使われているか分かりますか?
これがなければ今ごろ、日本の夏は地獄だったことでしょう…

・・・そうです。エアコンです。
これがなければ扇風機一台で夏を乗り切らなければなりません。
熱帯夜の日なんかは、ベッドが汗でべたべたになることでしょう…
というわけで、改めて、偉大な「ジュール・トムソンの実験」を解説していきます!
ジュール・トムソンの実験の概要
ここではまず、ジュール・トムソンの実験の設定を見ていきたいと思います。
実験の設定
下の図を見てください。
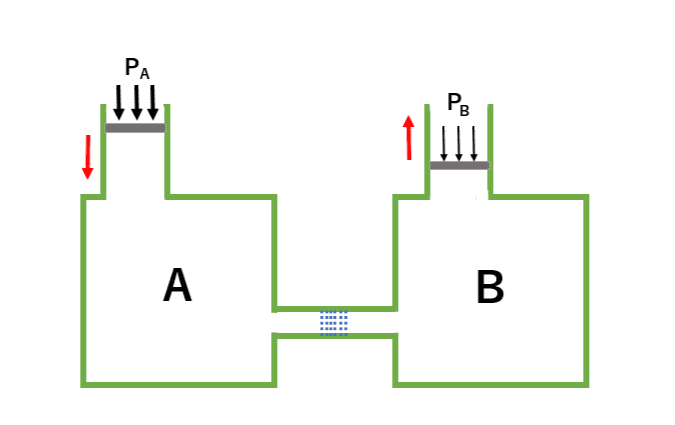
・容器A内の圧力は常に\(p_A\)で、容器B内の圧力は常に\(p_B\)
・\(p_A > p_B\)
・容器Aと容器Bに間で熱のやり取りはしない。容器の内外でもやり取りは無し。
・容器Aと容器Bの間は綿を詰めた連結管で繋がれていて、気体はゆっくり移動できる。
・容器A内の温度だけ一定に保つ。
実験の設定はこんな感じです。
実験を行うとどうなる?
\(p_A > p_B\)なので、容器Aに入っていた気体が、容器Bに流れ出ていきますね。
その結果、容器A内の気体の体積は減り、逆に容器B内の気体の体積は増えていきます。
大事なのは、「そのとき容器B内の温度はどうなるのか」、ということです。
上がるのか?それとも下がるのか?はたまた変わらないのか?
それを考えるために、まず、容器A, Bの温度、体積をそれぞれ\(T_A, V_A, T_B, V_B\)とおきます。
これらを使って、通過した気体の受けた内部エネルギー変化ΔUを考えてみましょう。
まず、この気体は圧力\(p_A\)で押し出されて出て行ったので、\(p_AV_A\)の仕事をされてます。
次に圧力\(p_B\)が掛かっているところへ押し入って行っているので、\(p_BV_B\)の仕事をしたことになります。
合計すると、気体がされた仕事は、\(W = p_BV_B – p_AV_A\)ですよね。
今回は断熱過程なので、気体は熱をやり取りしていません。Q=0です。
\(\Delta U = U_A – U_B = W + Q = p_BV_B – p_AV_A\)
ここから、
\(U_A + p_AV_A = U_B + p_BV_B\)
が分かります。
エンタルピーの式\(H = U + pV\)を思い出して、先ほどの式をよく見てみると、移動の前後でエンタルピーが変化していないことが分かります!
なので、エンタルピーHが一定の時、圧力を変化させると温度がどうなるかを調べればいいことになります。
ジュール・トムソン係数\(\mu _{JT}\)を、
\( \mu _{JT} = (\frac{\delta T}{\delta p})\)
と置くと、これの正負で温度が上がるか下がるかを知ることが出来ます。
例えば、\( \mu _{JT} = (\frac{\delta T}{\delta p}) > 0\)のときは、pが大きくなれば、Tも大きくなるので、断熱圧縮(\(\deltap > 0\))すると、温度が上がり、断熱膨張\(\deltap < 0\)させれば、温度が下がることが分かりますね!!
実際、空気ではほとんどの条件下で\( \mu _{JT} > 0\)が成り立つので、この操作を繰り返すと温度をどんどん下げられることが分かります!
ちなみに
ちなみに、理想気体だとどうなるのでしょうか?
答えは理想気体のとき、\( \mu _{JT} = (\frac{\delta T}{\delta p} = 0\)になるので、温度変化はなしです。
これにはジュール・トムソン係数についての式変形が必要になってくるので、またどこかでそれについて書きたいと思います。(この式変形にはマクスウェルの規則を使います)

コメント