今回は「簡約公式」に関する記事です。
おそらくこれを読んでいる人は分子の対称性を少しずつ学んできて、
「次は簡約公式について知りたい!」って考えている人がほとんどだと思います。
もし、「対称性とかSALCとかが知りたい…」って人はこちらもどうぞ。

というわけで、早速簡約公式について説明していきます!!
簡約公式とは?
教科書っぽく言うなら、簡約公式とは、「可約表現を既約表現に分解するための公式」です。
ここでいう「可約表現」と「既約表現」はそれぞれ、「対称種がまとまっている状態」と「対称種がバラバラになっている状態」みたいなイメージです。
式で表すと、
可約表現\(\Gamma\)の一般式を
\(\Gamma = c_1\Gamma_1 + c_2\Gamma_2 + ・・・\)
としたとき、
ci (i = 1, 2, …)を求めるための公式が簡約化の公式で、
\(\Large{c_i = \frac{1}{h}\displaystyle\sum_{C}^{}g(C)\chi_i(C)\chi(C)}\)
という風に表せます。
ただし、
\(h\):位数 ,\( g(C)\):その類の操作の数 , \(\chi_i(C):既約表現\Gamma_i\)の指標\(\chi_i , \chi(C)\):元々の可約表現\(\Gamma\)の対応する指標\(\chi\)
です。
…ややこしそうですね。でも、式は難しそうですが、実際の操作自体はそんなに難しくないです!
ここで確認ですが、対称種っていうのは、\(E, A_1\)みたいなやつです。
\(\Gamma\)という対称種を、\(\Gamma = E + A_1\)みたいに分解することを簡約化といいます。
これだけ聞いても、正直ピンとこないと思うので、実際に使うところを見ていきましょう!
公式は使ってナンボです!!
実際の使用方法
実際に問題を通して使い方を見ていきます。
\(\ce{cis-[PdCl2(NH3)2]}\)分子を考える。水素原子を無視すれば、この分子は点群\(C_{2v}\)に属する。
原子の変異によって張られる対称種は何か?
| C2v | E | C2 | σv(xz) | σv‘(yz) |
|---|---|---|---|---|
| A1 | 1 | 1 | 1 | 1 |
| A2 | 1 | 1 | -1 | -1 |
| B1 | 1 | -1 | 1 | -1 |
| B2 | 1 | -1 | -1 | 1 |
【解答前編】簡約公式を使う前の下準備
まず簡約公式を使う前に、5つの原子の5×3(←x, y, z)=15個の変位を考える必要があります。
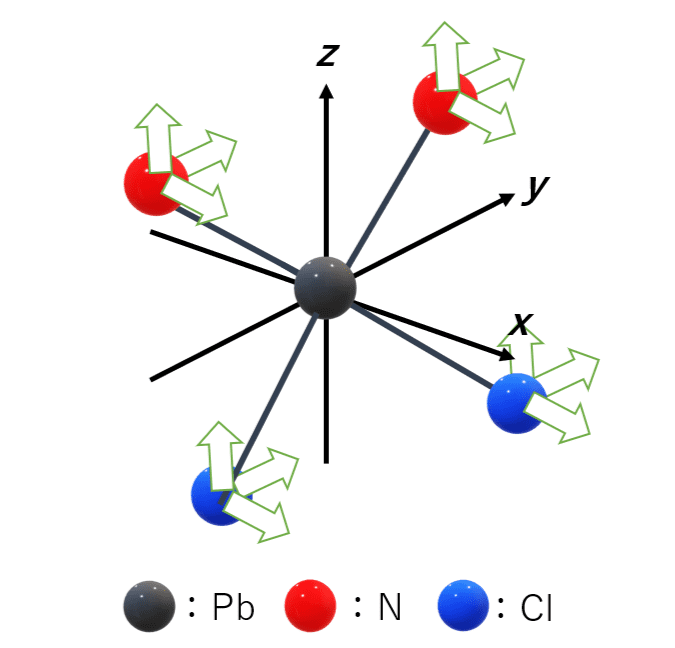
それぞれの対称操作でどう変わるかを見ていきましょう。
(復習になりますが、対称操作と寄与の関係は以下のようになります。)
- 同じ状態に残る変位は1の寄与
- 位置が同じで反転する変位はー1の寄与
- それ以外(位置が変わるなど)は0の寄与
Eの対称操作
当然ながら、5つの原子それぞれの3つの変位は変化しません
3×5 =15
C2の対称操作
位置が変わらないのはPdのみで、
z方向の変位は変化しませんが、x, y方向の変位は符号が反転します。
よって、1 + ( -1 ×-1) = -1
σv(xz)の対称操作
位置が変わらないのはPdのみで、
z, x方向の変位は変化しませんが。y方向の変位は符号が反転します。
よって、1×2 + (-1) =1
σv(yz)の対称操作
5つすべての原子が動きません。
y, z方向の変位は変化しませんが、x方向の変位は符号が反転します。
よって、5 ×(2 – 1) = 5
\(\Gamma\)の指標
以上より、\(\Gamma\)の指標は、
| E | C2 | σv(xz) | σv‘(yz) |
| 15 | -1 | 1 | 5 |
となります。
【解答後編】簡約公式の使用
下準備が終わったので、簡約公式を使っていきます!
(再掲【簡約公式と指標】)
\(c_i = \frac{1}{h}\displaystyle\sum_{C}^{}g(C)\chi_i(C)\chi(C)\)
| C2v | E | C2 | σv(xz) | σv‘(yz) |
|---|---|---|---|---|
| A1 | 1 | 1 | 1 | 1 |
| A2 | 1 | 1 | -1 | -1 |
| B1 | 1 | -1 | 1 | -1 |
| B2 | 1 | -1 | -1 | 1 |
まず、C2において対称操作は合計4つ(E, C2, σv(xz), σv‘(yz))あるので、h=4です。
次に、それぞれの対称操作の数は1回なので、g(C)=1です。
\(\chi_i(C)と\chi(C)\)は対称種ごとに変わるので、それぞれ見ていきます。
最初はA1から見ていきます。上の表より、A1は、4つの対称操作で寄与が全部1なので、
\(c_1 = \frac{1}{4}(1\times15 + 1\times(-1) + 1\times1 + 1\times5) = 5\)
よって、c1 = 5
次にA2では、
\(c_2 = \frac{1}{4}(1\times15 + 1\times(-1) + -1\times1 + -1\times5) = 2\)
よって、c2 = 2
同様にB1, B2 について、c3 = 3, c4 = 5
よって、\(\Large{\Gamma = 5A_1 + 2A_2 + 3B_1 + 5B_2}\)
これで簡約化できました!
あとがき
簡約公式は見た目が少々ゴツいし、用語が多くてこんがらがりそうですが、慣れれば意外と操作は簡単です。
まずは、問題を通して使い方をマスターしてください!

コメント